Diferansiyel ve İntegral Hesap: Kalkülüsün Temel Prensipleri ve Uygulamaları
Diferansiyel ve integral hesap, genel olarak kalkülüs adıyla bilinen matematiğin iki ana dalıdır. Diferansiyel ve integral hesap, değişim oranlarını ve birikimli değerleri analiz eden güçlü araçlar sunar ve bu yöntemler modern matematik, fizik, mühendislik, ekonomi ve birçok bilim dalında geniş bir şekilde kullanılır. Isaac Newton ve Gottfried Wilhelm Leibniz tarafından 17. yüzyılda geliştirilmiş olan kalkülüs, günümüzün temel matematiksel disiplinlerinden biridir. Bu makalede, diferansiyel ve integral hesabın ne olduğuna, temel prensiplerine ve uygulama alanlarına yakından bakacağız.
Diferansiyel Hesap Nedir?
Diferansiyel hesap, bir fonksiyonun değişim oranlarını inceleyen bir matematik dalıdır. Başka bir deyişle, bir fonksiyonun eğilimi veya bir noktadaki anlık değişimi anlamak için kullanılır. Bu süreç, türev adı verilen bir işlemle yapılır.
Türev Kavramı
Bir fonksiyonun türevi, o fonksiyonun belirli bir noktada ne kadar hızlı değiştiğini gösterir. Türev, bir eğrinin eğimi olarak da anlaşılabilir. Örneğin, bir cismin zaman içerisindeki konum değişimi incelenerek hızının bulunması, diferansiyel hesabın bir uygulamasıdır.
Türev, şu formülle gösterilir:
f′(x)=limh→0f(x+h)−f(x)hf'(x) = \lim_{h \to 0} \frac{f(x+h) – f(x)}{h}f′(x)=limh→0hf(x+h)−f(x)
Burada:
- f'(x), fonksiyonun türevi,
- h, sonsuz küçük bir değişikliktir.
Diferansiyel Hesap Uygulamaları
Diferansiyel hesap, fizik, mühendislik, biyoloji ve ekonomi gibi birçok alanda kullanılır. İşte bazı önemli uygulama alanları:
- Hız ve İvme: Fizikte, bir cismin hızını ve ivmesini hesaplamak için türevler kullanılır. Hız, konumun zaman göre türevi, ivme ise hızın zaman göre türevi ile hesaplanır.
- Maksimum ve Minimum Problemleri: Diferansiyel hesap, bir fonksiyonun maksimum veya minimum noktalarını bulmak için kullanılır. Ekonomide, bir işletmenin kârını maksimize etmek veya maliyetini minimize etmek gibi problemlerin çözümünde önemli bir araçtır.
- Optimizasyon: Mühendislikte, belirli bir sistemin en verimli şekilde çalışmasını sağlamak için diferansiyel hesap kullanılır.
İntegral Hesap Nedir?
İntegral hesap, bir fonksiyonun belirli bir aralıkta birikimli değerlerini bulmaya yarayan matematiksel bir yöntemdir. İntegral, birikim, alan veya hacim hesaplamalarında kullanılır. Diferansiyel hesap, anlık değişimleri incelerken, integral hesap birikimli değişimleri analiz eder.
İntegral Kavramı
Bir fonksiyonun integrali, o fonksiyonun altında kalan alanı hesaplamak için kullanılır. İki temel integral türü vardır:
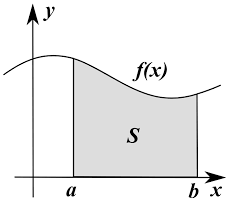
- Belirli İntegral: Bir fonksiyonun belirli iki nokta arasındaki toplam değişimini hesaplar. Matematiksel formülü şu şekildedir:∫abf(x)dx\int_{a}^{b} f(x) dx∫abf(x)dxBu, a ve b arasındaki alanı temsil eder.
- Belirsiz İntegral: Bir fonksiyonun türevini bulmak yerine, o fonksiyonun orijinal formunu yeniden elde etmek için kullanılır. Bu integral türü genel bir ifade sunar ve şu formülle gösterilir:∫f(x)dx=F(x)+C\int f(x) dx = F(x) + C∫f(x)dx=F(x)+CBurada C, entegrasyon sabitidir.
İntegral Hesap Uygulamaları
İntegral hesap, birçok bilim dalında yaygın bir şekilde kullanılmaktadır. İşte bazı uygulama alanları:
- Alan ve Hacim Hesaplama: İntegral hesap, bir eğri altında kalan alanı veya bir cismin hacmini hesaplamak için kullanılır. Bu, mühendislikte ve geometri problemlerinde önemli bir uygulamadır.
- Fiziksel Büyüklükler: Elektriksel akım, enerji, ve kütle merkezi gibi büyüklüklerin hesaplanmasında integraller kullanılır.
- Olasılık ve İstatistik: Olasılık teorisinde, sürekli rastgele değişkenlerin dağılım fonksiyonlarını hesaplamak için integral hesap kullanılır.
Diferansiyel ve İntegral Hesap Arasındaki İlişki
Diferansiyel ve integral hesap arasında önemli bir bağlantı vardır. Temel Kalkülüs Teoremi, bu iki kavramı birleştirir ve bir fonksiyonun türevinin, o fonksiyonun integralinin tersine dönüştürülebileceğini gösterir. Bu teorem, diferansiyel ve integral hesap arasındaki ilişkiyi şu şekilde açıklar:
- Bir fonksiyonun türevi alındığında, o fonksiyonun anlık değişim hızı bulunur.
- Aynı fonksiyonun integrali alındığında, o fonksiyonun altında kalan alan hesaplanır.
Bu teorem, diferansiyel ve integral hesapları birbirinin tamamlayıcısı yapar.
Diferansiyel ve İntegral Hesap Nerelerde Kullanılır?
Diferansiyel ve integral hesap, çeşitli bilim dallarında ve endüstrilerde kritik öneme sahiptir. İşte bazı örnekler:
- Fizik: Hareket, kuvvet, enerji ve elektrik devreleri gibi konular diferansiyel ve integral hesap kullanılarak analiz edilir.
- Mühendislik: Mühendislik projelerinde, yapısal analizden akışkanlar mekaniğine kadar pek çok alanda diferansiyel ve integral hesaplama teknikleri kullanılır.
- Ekonomi ve Finans: Fiyatların değişim hızı, enflasyon hesaplamaları, maksimum kâr analizi ve maliyet minimizasyonu gibi problemler diferansiyel hesapla çözülürken, toplam maliyet ve gelir analizleri için integral hesap kullanılır.
- Biyoloji ve Kimya: Biyolojik süreçlerin modellemesi, kimyasal reaksiyonlar ve popülasyon dinamikleri gibi konularda diferansiyel denklemler ve integral hesaplama teknikleri uygulanır.
Sonuç
Diferansiyel ve integral hesap, matematiğin en güçlü araçları arasında yer almakta olup, bilim ve teknolojinin gelişmesinde büyük bir rol oynamıştır. Diferansiyel hesap, bir fonksiyonun değişim hızını anlamaya yardımcı olurken, integral hesap birikimli değerleri bulmayı sağlar. Bu iki hesaplama yöntemi, modern dünyada fizik, mühendislik, ekonomi, biyoloji ve diğer pek çok alanda kullanılmaktadır. Kalkülüs, bu iki yöntemin birleşimiyle, karmaşık sistemlerin analiz edilmesine ve çözülmesine olanak tanıyan temel bir matematiksel disiplindir.